
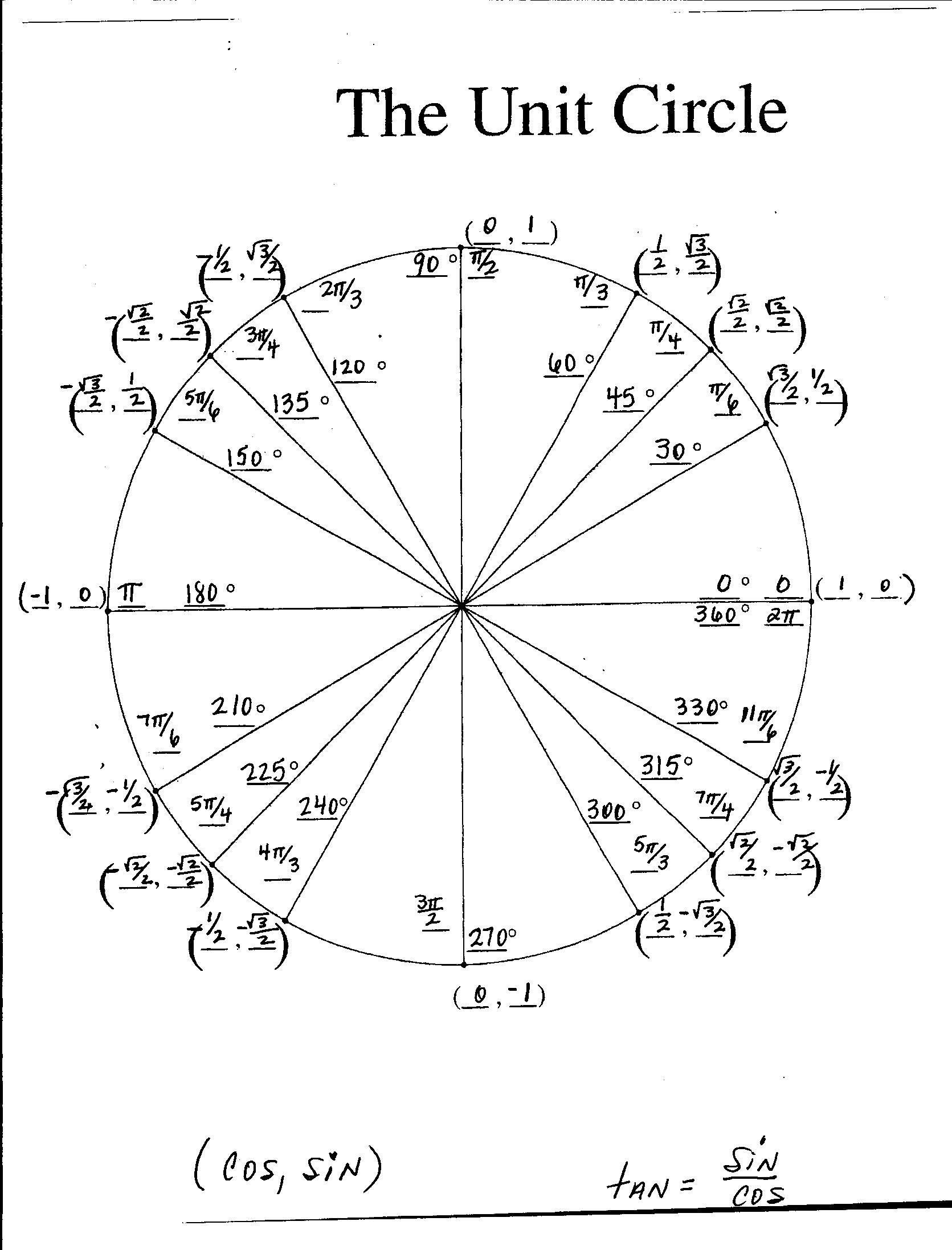
IUNIT CIRCLE HOW TO
Show them how to extend their knowledge to eagles like 0 degrees and 90 degrees so that they’ll be prepared for looking at angles greater than 180 degrees or less than 0 degrees in the next lesson. A unit circle is just a circle that has a radius with a length of 1. Again, it’s important that students understand why the cosine is the x-coordinate and the sine is the y-coordinate, so be sure to keep referring back to the ratios from the triangles throughout the debrief. The sequencing of questions in this lesson was developed strategically so the students would understand the concept behind “the unit circle” and how it helps us evaluate trigonometric ratios for specific angles. These Chart Templates carry spaces to be customized with your specific data. It can be used for a quiz as it will test the students competitively.

This Unit circle chart will help to understand the angle in the circle, the approximate radian value and the exact radian value.
IUNIT CIRCLE PDF
In number three, they’ll develop the understanding of the first quadrant of the unit circle as it relates to evaluating sine, cosine, and tangent of different angles. Unti Circle Chart Free PDF Template Download. The idea here is that students don’t get caught up in “Sine = y and cosine = x,” but they keep up with the understanding that sine is the ratio of the opposite side to the hypotenuse and cosine is the ratio of the adjacent side to the hypotenuse. This will lead them to the unit circle, where the radius is 1 and the values of sine and cosine at different angles are equal to the x- and y-coordinates at those spots. Multiple choice questions on unit circle in trigonometry with answers at the bottom of the page. Home Questions on Unit Circles in Trigonometry.
We want them to see that when the hypotenuse is 1, the actual side length of the triangles are the same as the sine and cosine ratios for specific angles. A unit circle chart is a 1-unit radius circle with a center (0, 0) of the Cartesian plane used in trigonometry to determine the sine and cosine values of angles. These questions helps in understanding the use of the unit circle. So this height right over here is going to be equal to b. Well, this height is the exact same thing as the y-coordinate of this point of intersection. In numbers 1 and 2, the students will write ratios for sine and cosine when given a triangle with all of the side lengths. Now, what is the length of this blue side right over here You could view this as the opposite side to the angle.


 0 kommentar(er)
0 kommentar(er)
